FACTORIZACIÓN.

FACTORIZACION

• 

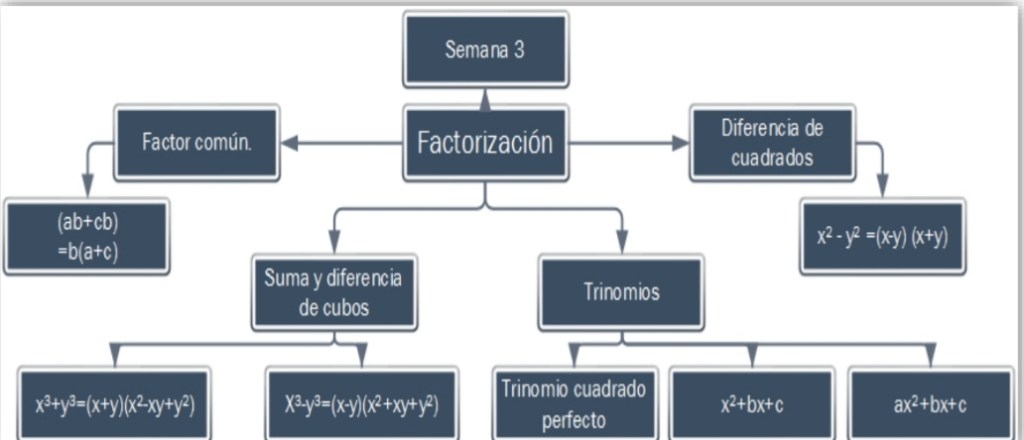
Tema 1. Factor común

Si varios sumandos tienen un factor común, podemos transformar la suma en producto extrayendo dicho factor. Sacar factor común es el proceso inverso a la propiedad distributiva.
Para poder sacar factor común hay que tener presente la propiedad distributiva del producto respecto a la operación.

Ejercicios:
1) 20x^5-25x^4+30x^2
2) 4m^2-12mn-5m+15n
3) 3/8 x^6-15/4 x^7 a

Tema 2. Diferencia de cuadrados

Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta. Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.
Los pasos para desarrollar la diferencia de cuadrados perfectos son:
1.Extraer la raíz cuadrada de ambos términos.
2.Se multiplica la suma por la diferencia de estas cantidades.

Ejercicios:
1) 81-46x^2
2) 144/x^6 -b^2
3) 36x² – a⁶b⁴

Tema 3. Suma y diferencia de cubos

La suma de dos cubos perfectos se descompone en dos factores, el primero es la suma de sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz menos el producto de ambas raíces más el cuadrado de la segunda raíz.

La fórmula a usar al momento de factorizar una suma de cubos es la siguiente:
x³+y³=(x+y)(x²-xy+y²)

La diferencia de dos cubos perfectos se descompone en dos factores, el primero es la diferencia de sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz más el producto de ambas raíces más el cuadrado de la segunda raíz.

La fórmula a usar al momento de factorizar una diferencia de cubos es la siguiente:
x³-y³=(x-y)(x²+xy+y²)

Ejercicios
1) 512-27x^9
2) 64x^3-729
3) 8a^3+b^3
4) 27a^3+8

Tema 4. Trinomios

Trinomio cuadrado perfecto

Se le llama Trinomio cuadrado perfecto al trinomio (polinomio de tres términos) tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.

Para que sea un trinomio cuadrado perfecto debe de cumplir 4 reglas

1) Tiene que tener 3 términos.
2) El primer y tercer término sean positivos.
3) Primero y tercer término tengan raíz cuadrada exacta.
4) El segundo término sea el doble producto del primero y el tercero.

Trinomio de la forma x²+bx+c

Reglas para factorizar un trinomio de esta forma:

1. Se descompone el trinomio en dos factores binomios cuyo primer término será la raíz cuadrada del término x².
2. El signo del primer binomio será el mismo signo que tenga el término “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.
3. Si los dos factores tienen signos iguales entonces se buscan dos números cuya suma sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, estos números son los segundos términos de los factores binomios.
4. Si los dos factores tienen signos diferentes entonces se buscan dos números cuya diferencia sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, el mayor de estos números será el segundo término del primer factor binomio, y el menor de estos números será el segundo término del segundo factor binomio.

Trinomio de la forma ax²+bx+c

Este tipo de trinomio se diferencia del anterior debido a que el termino al cuadrado x² se encuentra precedido por un coeficiente diferente de uno (debe ser positivo).
Pasos para desarrollar este tipo de trinomios

1. Multiplicamos el coeficiente “a” del factor “ax²” por cada termino del trinomio, dejando esta multiplicación indicada en el término “bx” de la manera “b(ax)”, y en el término “ax²” de la manera ax².
2. Se descompone el trinomio en dos factores binomios cuyo primer término será la raíz cuadrada del término ax² la que sería “ax”.
3. Al producto resultante lo dividimos entre el factor “a”, con el fin de no variar el valor del polinomio.
4. El signo del primer binomio será el mismo signo que tenga el término “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.
5. Se buscaran los segundos términos de los binomios según los pasos tres y cuatro del caso del trinomio anterior.