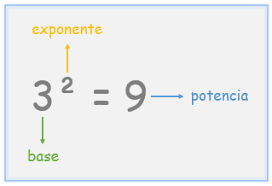
POTENCIAS DE UN EPONENTE ENTERO

El exponente de una potencia puede ser un número entero y tener por tanto signo positivo o negativo.

Una potencia de signo negativo es igual a 1 dividido por la misma potencia con signo positivo:

X^-n = 1 / Xⁿ

Veamos un ejemplo:

4^-3 = 1 / 4³

1.- Propiedades de las potencias:

1.– El producto de 2 potencias con diferentes bases e iguales exponentes es igual al producto de sus bases manteniendo el mismo exponente.

3³x5³= 15³

2.– La división de 2 potencias con diferentes bases e iguales exponente es igual a la división de sus bases manteniendo el mismo exponente.

12²:4²= 3²

3.– El producto de 2 potencias con iguales bases y diferentes exponentes es igual a la misma base siendo su exponente la suma de los exponentes.

4³x4⁵= 4^{3 + 5}= 4⁸

4.– La división de 2 potencias con iguales bases y diferentes exponentes es igual a la misma base siendo su exponente la resta de los exponentes.

5⁶:5⁴= 5^{6 – 4}= 5²

5.– Una potencia elevada a otra potencia mantiene la misma base siendo el exponente el producto de sus exponentes.

( 5²)³= 5^{2 x 3}= 5⁶

6.– Una fracción elevada a un exponente es igual a numerador y denominador elevados a dicho exponente.

( 2 / 6)³= 2³ / 6³

7.– Una fracción elevada a un exponente negativo es igual a la fracción inversa elevada al exponente positivo.

( 2 / 6)^-3= ( 6 / 2)³

2.- Operaciones con potencias

A la hora de resolver operaciones combinadas el orden de resolución es el siguiente:

1.- Los paréntesis, comenzando por los paréntesis interiores

2.- Las potencias

3.- Las multiplicaciones y las divisiones

4.- Las sumas y las restas.

Veamos algunos ejemplos:

1º ejemplo:

(2 / 3)² x (2 / 3)^-2=

(2 / 3)²x (3 / 2)² = (En rojo: la potencia negativa de una fracción es igual a la potencia positiva de la fracción inversa)

(2 / 3 x 3 / 2)² = (En negrita: el producto de dos potencias de igual exponente es igual al producto de sus bases elevado a dicho exponente)

(6 / 6)² = 1

2º ejemplo:

(4²)³ – 4⁶ =

4⁶ – 4⁶ = 0 (En negrita: una potencia elevada a otra potencia es igual a la base elevada al producto de sus exponentes)

3º ejemplo:

3²x 3⁴ – (1 / 3)^-6 =

3²⁺⁴– (3 / 1)⁶ = (En negrita: el producto de dos potencias de la misma base es otra potencia de la misma base elevada a la suma de los exponentes; En azul: la potencia negativa de una fracción es igual a la potencia positiva de la fracción inversa)

3⁶ – 3⁶ = 0

4º ejemplo:

((5 / 7)² – (7 / 4)^-2)³ / (3 / 7)³ =

((5 / 7)² – (4 / 7)²)³ / (3 / 7)³ = (En negrita: la potencia negativa de una fracción es igual a la potencia positiva de la fracción inversa)

(5² / 7² – 4² / 7²)³ / (3 / 7)³ = (En negrita: la potencia de una fracción es igual a numerador y denominador elevados a dicha potencia)

((5² – 4²) / 7²)³ / (3 / 7)³ = (En negrita: restamos dos potencias de igual denominador)

(3² / 7²)³ / (3 / 7)³ = (En negrita: simplificamos 5² – 4²= 9 = 3²)

((3² x 7) / (7² x 3))³ = (En negrita: para dividir dos potencias de igual exponente se dividen las bases y se mantiene el mismo exponente)

(3 / 7)³ = 3³ / 7³

3.- Potencias con exponente racional

El exponente de una potencia puede ser una fracción:

5 ^{2 / 3}

Estas potencias son equivalentes a una raíz cuyo índice es el denominador de la fracción, siendo el radicando la base de la potencia y su exponente el numerador:

EXPLICACIÓN DE LAS PROPIEDADES

EXPLICACIÓN DE LAS POTENCIAS

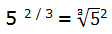
RADICALES

Radical es un adjetivo que puede referirse a aquello perteneciente o relativo a la raíz, a algo (un giro, un cambio) total o completo, o a aquella persona partidaria de reformas extremas o que suele ser tajante o intransigente.

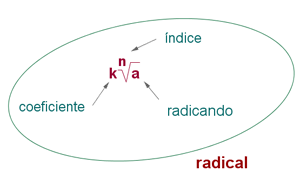
Un radical es una expresión de la forma $\sqrt[n]{a}$ , en la que $n \in \mathbb{N}$ y $a \in \mathbb{R}$ . Además, si es par, entonces no puede ser negativo $(a \geq 0)$ .

Por ejemplo, tenemos que es par. Por lo tanto, $\sqrt{64} = 8$ ; mientras que $\sqrt{-64} \notin \mathbb{R}$ .

Asimismo, como es impar, entonces $\sqrt[3]{8} = 2$ y $\sqrt[3]{-8} = -2$ . Es decir, la raíz cúbica está definida para cualquier número real

Se puede expresar un radical en forma de potencia:

Ejemplo:

Ponemos en forma de potencia al 256 , 256 = 2^8

El índice del radical (2) se transforma en el denominador y el exponente del radicando (8) en el numerador y efectuamos las operaciones:

\displaystyle \sqrt{256} = \sqrt{2^8} = 2^{8/2} = 2^4 = 16

Simplificación de radicales

Si existe un número natural que divida al índice y al exponente (o los exponentes) del radicando, se obtiene un radical simplificado.

Ejemplos

1 Simplificar $\sqrt[6]{256}$

Ponemos en forma de potencia al 256 , 256 = 2^8

Para simplificar el radical dividimos por tanto el índice (6) como el exponente del radicando (8)

\sqrt[6]{256}= \sqrt[6]{2^8} = \sqrt[3]{2^4}

2 Simplificar $\displaystyle \sqrt[4]{2^6 \cdot 3^{10} }$

Para simplificar el radical dividimos por tanto el índice (4) como los exponentes del radicando $(6 \textup{ y }10)$

\displaystyle \sqrt[4]{2^6 \cdot 3^{10} }= \sqrt{2^3 \cdot 3^5}

Reducción a índice común

Para reducir a común índice dos a más radicales:

1 Hallamos el mínimo común múltiplo de los índices, que será el común índice

2 Dividimos el común índice por cada uno de los índices y cada resultado obtenido se multiplica por sus exponentes correspondientes

Ejemplo:

Poner a común índice los radicales:

\displaystyle \sqrt{2}, \quad \sqrt[3]{2^2 \cdot 3^2}, \quad \sqrt[4]{2^2 \cdot 3^3}

En primer lugar hallamos el m.c.m. de los índices: 2, 3 y

Dividimos el común índice (12) por cada uno de los índices (2, 3 y y cada resultado obtenido se multiplica por sus exponentes correspondientes

\displaystyle \sqrt[12]{2^6}, \quad \sqrt[12]{(2^2)^4 \cdot (3^2)^4}, \quad \sqrt[12]{(2^2)^3 \cdot (3^3)^3}

Operamos con las potencias

\displaystyle \sqrt[12]{2^6}, \quad \sqrt[12]{2^8 \cdot 3^8}, \quad \sqrt[12]{2^6 \cdot 3^9}

Extracción de factores en un radical

Para extraer factores de un radical se descompone el radicando en factores. Si:

Un exponente del radicando es menor que el índice

El factor correspondiente se deja en el radicando.

Ejemplos:

1 $\displaystyle \sqrt{6} = \sqrt{2 \cdot 3}$

2 $\displaystyle \sqrt[3]{9} = \sqrt[3]{3^2}$

Un exponente del radicando es igual al índice

El factor correspondiente sale fuera del radicando.

Ejemplos:

1 $\displaystyle \sqrt{12} = \sqrt{2^2 \cdot 3} = 2 \sqrt{3}$

Descomponemos en factores, como el está elevado a la misma potencia que el índice podemos extraer el del radicando

2 $\displaystyle \sqrt[3]{8} = \sqrt[3]{2^3} = 2$

Descomponemos en factores, como el está elevado a la misma potencia que el índice podemos extraer el del radicando

Un exponente del radicando es mayor que el índice

Se divide dicho exponente por el índice. El cociente obtenido es el exponente del factor fuera del radicando y el resto es el exponente del factor dentro del radicando

Ejemplos:

1 $\sqrt{48}$

El exponente del 2 es mayor que el índice, por tanto se divide dicho exponente (4) entre el índice (2)

\sqrt{48}= \sqrt{2^4 \cdot 3} = 2^2\sqrt{3} = 4 \sqrt{3}

El cociente obtenido (2) es el exponente del factor fuera del radicando y el resto (0) es el exponente del factor dentro del radicando.

Como el factor 2^0 es igual a 1, no es necesario colocarlo en el radicando ya que si se multiplica por otro factor este no varía

En general, si el resultado de dividir el exponente de un factor por el índice da como resto cero, no colocaremos ese factor en el radicando

2 $\sqrt[3]{243}$

Descomponemos en factores: 243 = 3^5

El exponente es mayor que el índice, por tanto se divide dicho exponente (5) entre el índice (3) .

El cociente obtenido (1) es el exponente del factor fuera del radicando y el resto (2) es el exponente dentro del radicando

\sqrt[3]{243}= \sqrt[3]{3^5} = 3\sqrt[3]{3^2} = 3 \sqrt[3]{9}

3 $\sqrt{2 \cdot 3^2 \cdot 5^5}$

Hay exponentes en el radicando mayores que el índice, por tanto se dividen dichos exponentes y por el índice (2) .

Cada uno de los cocientes y obtenidos será el exponente del factor correspondiente fuera del radicando y cada uno de los restos obtenidos y serán los exponentes de los factores correspondientes dentro del radicando

\sqrt{2 \cdot 3^2 \cdot 5^5} = 3 \cdot 5^2 \cdot \sqrt{2 \cdot 5} = 75 \sqrt{10}

4 $\displaystyle \sqrt[4]{2^7 \cdot 3^{14} \cdot 5^4} = 2 \cdot 3^3 \cdot 5 \cdot \sqrt[4]{2^3 \cdot 3^2} = 270\sqrt[4]{72}$

Los exponentes el radicando son mayores que el índice, por tanto se dividen dichos exponentes (7, 14 y por el índice (4) .

Cada uno de los cocientes (1, 3, 1) obtenidos será el exponente del factor correspondiente fuera del radicando y cada uno de los restos obtenidos (3, 2, 0) serán los exponentes de los factores correspondientes dentro del radicando

Introducción de factores en un radical

Para introducir factores en un radical se elevan los factores al índice del radical.

\displaystyle a \sqrt[n]{b} = \sqrt[n]{a^n b}

Ejemplos:

1 $\displaystyle 2\sqrt{3}$

Como el índice es , el factor fuera del radical (2) se eleva al cuadrado y realizamos las operaciones

\displaystyle 2\sqrt{3} = \sqrt{2^2 \cdot 3} = \sqrt{12}

2 $\displaystyle 2^2 \cdot 3^3 \sqrt[4]{6}$

Tanto el 2^2 como el 3^3 se introducen elevados a la cuarta potencia, es decir,

\displaystyle \sqrt[4]{(2^2)^4 \cdot (3^3)^4 \cdot 2 \cdot 3}

Quitamos los paréntesis multiplicando los exponentes

\displaystyle 2^2 \cdot 3^3 \sqrt[4]{2 \cdot 3} = \sqrt[4]{2^9 \cdot 3^{13} }

Multiplicamos las potencias con la misma base

Suma de radicales

Solamente pueden sumarse (o restarse) dos radicales cuando son radicales semejantes, es decir, si son radicales con el mismo índice e igual radicando.

Para sumar radicales con el mismo índice e igual radicando se se suman los coeficientes de los radicales.

\displaystyle a\sqrt[n]{k} + b\sqrt[n]{k} + c\sqrt[n]{k} = (a + b + c)\sqrt[n]{k}

Ejemplos:

1 $\displaystyle 2\sqrt{2} - 4\sqrt{2} + \sqrt{2}$

Sumamos los coeficientes de los radicales

\displaystyle (2 - 4 + 1)\sqrt{2} = -\sqrt{2}

2 $\displaystyle 3\sqrt[4]{5} - 2\sqrt[4]{5} - \sqrt[4]{5}$

Sumamos los coeficientes de los radicales

\displaystyle (3 - 2 - 1)\sqrt[4]{5} = 0

3 $\displaystyle \sqrt{12} - 3\sqrt{3} + 2\sqrt{75}$

Descomponemos en factores los radicandos:

\displaystyle 12 = 2^2 \cdot 3, \quad 75 = 3 \cdot 5^2

De manera que las raíces son

\displaystyle \sqrt{2^2 \cdot 3} - 3 \sqrt{3} + 2\sqrt{5^2 \cdot 3}

Extraemos factores de los radicales y los multiplicamos por el coeficiente del radical correspondiente

\displaystyle 2\sqrt{3} - 3\sqrt{3} + 10\sqrt{3}

Sumamos los coeficientes de los radicales

4 $\displaystyle \sqrt[4]{4} + \sqrt[6]{8} - \sqrt[12]{64}$

Extraemos factores de los radicales y los multiplicamos por el coeficiente del radical correspondiente

\displaystyle 4 = 2^2, \quad 8 = 2^3, \quad 64 = 2^8

De manera que

\displaystyle \sqrt[4]{2^2} + \sqrt[6]{2^3} - \sqrt[12]{2^6}

Simplificamos los radicales. En el primer radical dividimos el índice y el exponente del radicando por , en el segundo por y en el tercero por

\displaystyle \sqrt{2} + \sqrt{2} - \sqrt{2}

Sumamos los coeficientes de los radicales

Ejemplos de ejercicios de suma y resta de radicales

\displaystyle 2\sqrt{12} - 3\sqrt{75} + \sqrt{27}

Multiplicación de radicales con el mismo índice

Para multiplicar radicales con el mismo índice se multiplican los radicandos y se deja el mismo índice.

\displaystyle \sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{a \cdot b}

Multiplicación de radicales con distinto índice

Primero se reducen a común índice y luego se multiplican.

Ejemplos:

1 $\displaystyle \sqrt{3} \cdot \sqrt[3]{9} \cdot \sqrt[4]{27} =$

Descomponemos en factores los radicandos

\displaystyle = \sqrt{3} \cdot \sqrt[3]{3^2} \cdot \sqrt[4]{3^3}

Reducimos a común índice por lo que tenemos que calcular el mínimo común múltiplo de los índices, que será el común índice.

Dividimos el común índice (12) por cada uno de los índices (2, 3 ,4) y cada resultado obtenido se multiplica por sus exponentes correspondientes (1, 2 ,3) . Realizamos el producto de potencias con la misma base en el radicando y extraemos factores del radicando

\displaystyle = \sqrt[12]{3^6} \cdot \sqrt[12]{\left( 3^2 \right)^4} \cdot \sqrt[12]{\left( 3^3 \right)^3} = \sqrt[12]{3^6 \cdot 3^8 \cdot 3^9} = \sqrt[12]{3^{23}} = 3 \sqrt[12]{3^{11}}

División de radicales con el mismo índice

Para dividir radicales con el mismo índice se dividen los radicandos y se deja el mismo índice.

\displaystyle \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}

Ejemplo:

\displaystyle \frac{\sqrt[6]{128}}{\sqrt[6]{16}} = \sqrt[6]{\frac{128}{16}} = \sqrt[6]{\frac{2^7}{2^4}} = \sqrt[6]{2^3} = \sqrt{2}

Como los dos radicales tienen el mismo índice lo ponemos todo en un radical con el mismo índice

Descomponemos en factores, hacemos la división de potencias con la misma base

Simplificamos el radical dividiendo el índice y el exponente del radicando por

División de radicales con distinto índice

Primero se reducen a índice común y luego se dividen.

Ejemplos:

1 $\displaystyle \frac{\sqrt[3]{4}}{\sqrt{2}} =$

En primer reducimos a común índice por lo que tenemos que calcular el mínimo común múltiplo de los índices, que será el común índice. $\text{m.c.m.}(3, 2) = 6$ .

Dividimos el común índice (6) por cada uno de los índices ( y ) y cada resultado obtenido se multiplica por sus exponentes correspondientes ( y )

Descomponemos el en factores para poder hacer la división de potencias con la misma base y dividimos

\displaystyle \frac{\sqrt[3]{4}}{\sqrt{2}} = \sqrt[6]{\frac{4^2}{2^3}} = \sqrt[6]{\frac{\left(2^2 \right)^2}{2^3}} = \sqrt[6]{\frac{2^4}{2^3}} = \sqrt[6]{2}

Potencia de un radical

Para elevar un radical a una potencia, se eleva a dicha potencia el radicando y se deja el mismo índice.

\displaystyle \left( \sqrt[n]{a} \right)^m = \sqrt[n]{a^m}

Ejemplo:

1 $\displaystyle \left( \sqrt[3]{18} \right)^2 =$

Elevamos el radicando al cuadrado, descomponemos en factores y los elevamos al cuadrado y por último extraemos factores

\displaystyle\left(\sqrt[3]{18} \right)^{2}=\sqrt[3]{18^{2}}=\sqrt[3]{(2\cdot 3^2)^2}=\sqrt[3]{2^2\cdot 3^4}=3\sqrt[3]{12}

Raíz de un radical

La raíz de un radical es otro radical de igual radicando y cuyo índice es el producto de los dos índices.

\displaystyle \sqrt[n]{\sqrt[m]{a}}=\sqrt[n\dot m]{a}

Ejemplo:

1 $\displaystyle \sqrt{\sqrt[3]{\sqrt[4]{2}}}$

Multiplicamos los índices

\displaystyle \sqrt{\sqrt[3]{\sqrt[4]{2}}}=\sqrt[24]{2}

2 $\displaystyle \sqrt{2\sqrt[3]{2\sqrt[4]{2}}}$

Introducimos el primer dentro de la raíz cúbica por lo que tendremos que elevarlo al cubo y multiplicamos las potencias con la misma base

\displaystyle \sqrt{2\sqrt[3]{2\sqrt[4]{2}}}=\sqrt{\sqrt[3]{2^{3}\cdot 2\sqrt[4]{2}}}=\sqrt{\sqrt[3]{2^{4}\sqrt[4]{2}}}

Introducimos el 2^4 en la raíz cuarta por lo que tenemos que elevarlo a la cuarta, realizamos el producto de potencias y por último el producto de los índices

\displaystyle \sqrt{\sqrt[3]{\sqrt[4]{(2^{4})^{4}\cdot 2}}}=\sqrt[24]{2^{17}}

RACIONALIZACIÓN

RACIONALIZACIÓN

Racionalización

La racionalización de radicales consiste en quitar los radicales del denominador, lo que permite facilitar el cálculo de operaciones como la suma de fracciones

Podemos distinguir tres casos:

Caso 1

Racionalización del tipo $\displaystyle \frac{a}{b\sqrt{c}}$

Se multiplica el numerador y el denominador por $\displaystyle \sqrt{c}$

\displaystyle \frac{a}{b\sqrt{c}}=\frac{a\cdot \sqrt{c}}{b\sqrt{c}\cdot \sqrt{c}}=\frac{a\cdot \sqrt{c}}{b\left(\sqrt{c}\right)^{2}}=\frac{a\cdot \sqrt{c}}{b\cdot c}

Ejemplos:

\displaystyle \frac{2}{3\sqrt{2}}=\frac{2\cdot \sqrt{2}}{3\sqrt{2}\cdot \sqrt{2}}=\frac{2\cdot \sqrt{2}}{3\left(\sqrt{2}\right)^{2}}=\frac{2\cdot \sqrt{2}}{3\cdot 2}=\frac{\sqrt{2}}{3}

DENOMINADORES.

Caso 2

Racionalización del tipo $\displaystyle \frac{a}{b\sqrt[n]{c^{m}}}$

Se multiplica numerador y denominador por $\displaystyle \sqrt[n]{c^{n-m}}$

\displaystyle \frac{a}{b\sqrt[n]{c^{m}}}=\frac{a\cdot \sqrt[n]{c^{n-m}}}{b\sqrt[n]{c^{m}}\cdot \sqrt[n]{c^{n-m}}}=\frac{a\cdot \sqrt[n]{c^{n-m}}}{b \sqrt[n]{c^{m}\cdot c^{n-m}}}=\frac{a\cdot \sqrt[n]{c^{n-m}}}{b\cdot c}

Ejemplo:

\displaystyle \frac{2}{3\sqrt[5]{4}}=\frac{2}{3\sqrt[5]{2^{2}}}=\frac{2\cdot \sqrt[5]{2^{3}}}{3\sqrt[5]{2^{2}}\cdot \sqrt[5]{2^{3}}}=\frac{2\cdot \sqrt[5]{2^{3}}}{3 \sqrt[5]{2^{2}\cdot 2^{3}}}=\frac{2\cdot \sqrt[5]{2^{3}}}{3\cdot 2}=\frac{\sqrt[5]{8}}{3}

El radicando lo ponemos en forma de potencia: $2^{2}$

Tenemos que multiplicar en el numerador y denominador por la raíz quinta de $2^{5-2} = 2^{3}$

Multiplicamos los radicales del denominador, extraemos factores del radical y simplificamos la fracción

Caso 3

Racionalización del tipo $\displaystyle \frac{a}{\sqrt{b}+\sqrt{c}}$

Y en general cuando el denominador sea un binomio con al menos un radical.

Se multiplica el numerador y denominador por el conjugado del denominador.

El conjugado de un binomio es igual al binomio con el signo central cambiado:

\begin{array}{rcl} a+b & \longrightarrow & a-b \\ && \\ -a+b & \longrightarrow & -a-b \\ && \\ a-b & \longrightarrow & a+b \\ && \\ -a-b & \longrightarrow & -a-b \end{array}

También tenemos que tener en cuenta que: «suma por diferencia es igual a diferencia de cuadrados«.

Ejemplos:

1 $\displaystyle \frac{2}{\sqrt{2}-\sqrt{3}}$

Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados