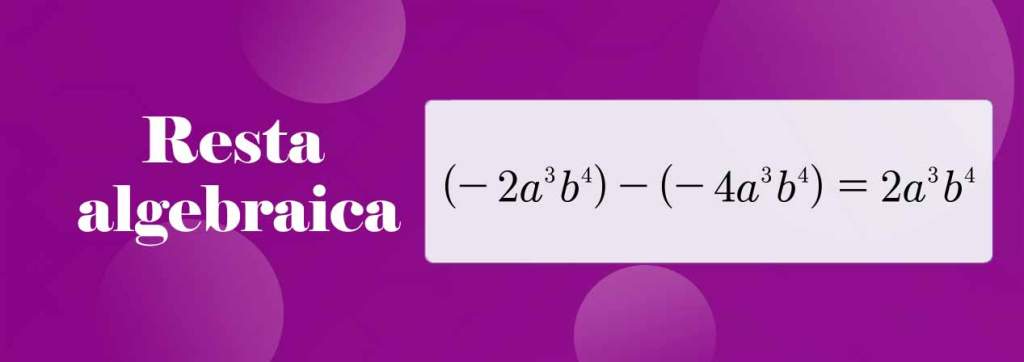EXPRESIONES ALGEBRAICAS
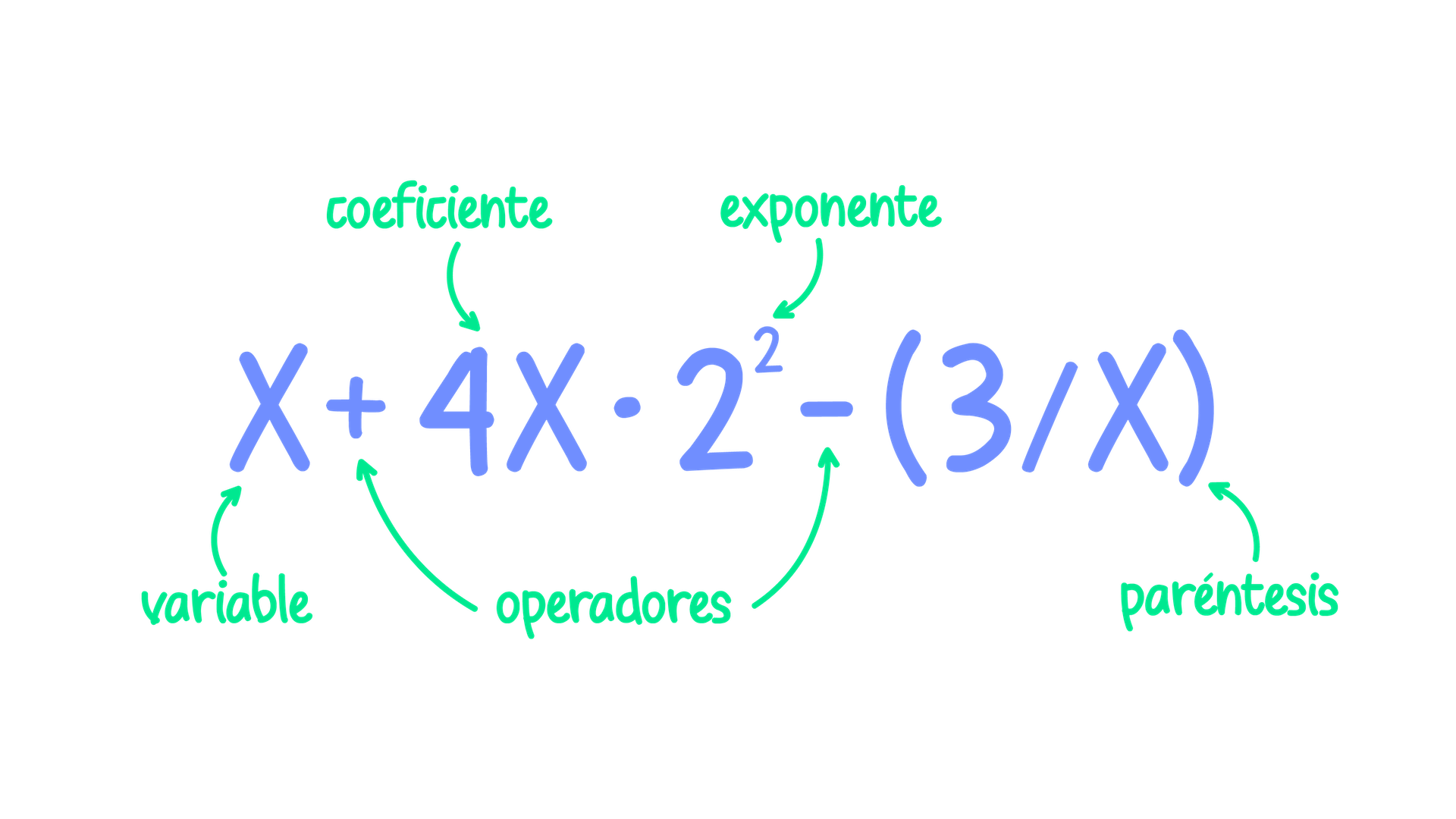
Cuando se trabaja en algebra se esta hablando de manejar relaciones numericas en la que una o mas cantidades son desconocidas. Las cuales son llamadas incognitas, variables o indeterminadas, que suelen representar con letras de la A-Z aunque la mas comun casi siempre es X.
Valor numerico.
El valor numérico de una expresión algebraica es el número que resulta de sustituir las variables de la de dicha expresión por valores concretos y completar las operaciones. Una misma expresión algebraica puede tener muchos valores numéricos diferentes, en función del número que se asigne a cada una de las variables de la misma
La única precaución necesaria es respetar el orden y las propiedades de las operaciones. Por ejemplo, no tiene sentido calcular el valor numérico de 1/x para 
, porque no se puede dividir entre cero.
En el siguiente ejemplo puedes ver cómo se haría la sustitución para calcular el valor numérico de para x=2 y= -1 z=4
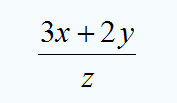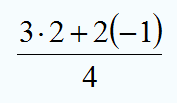
Faltaría completar las operaciones (el resultado final es 
), pero lo más importante es que te fijes en los elementos que se añaden al hacer la sustitución: Se sustitulle en el punto de la x el valor de 2 en la y el valor de -1 y en la z el valor de 4 como indica el ejercicio.
EXPRESIONES ALGEBRAICAS
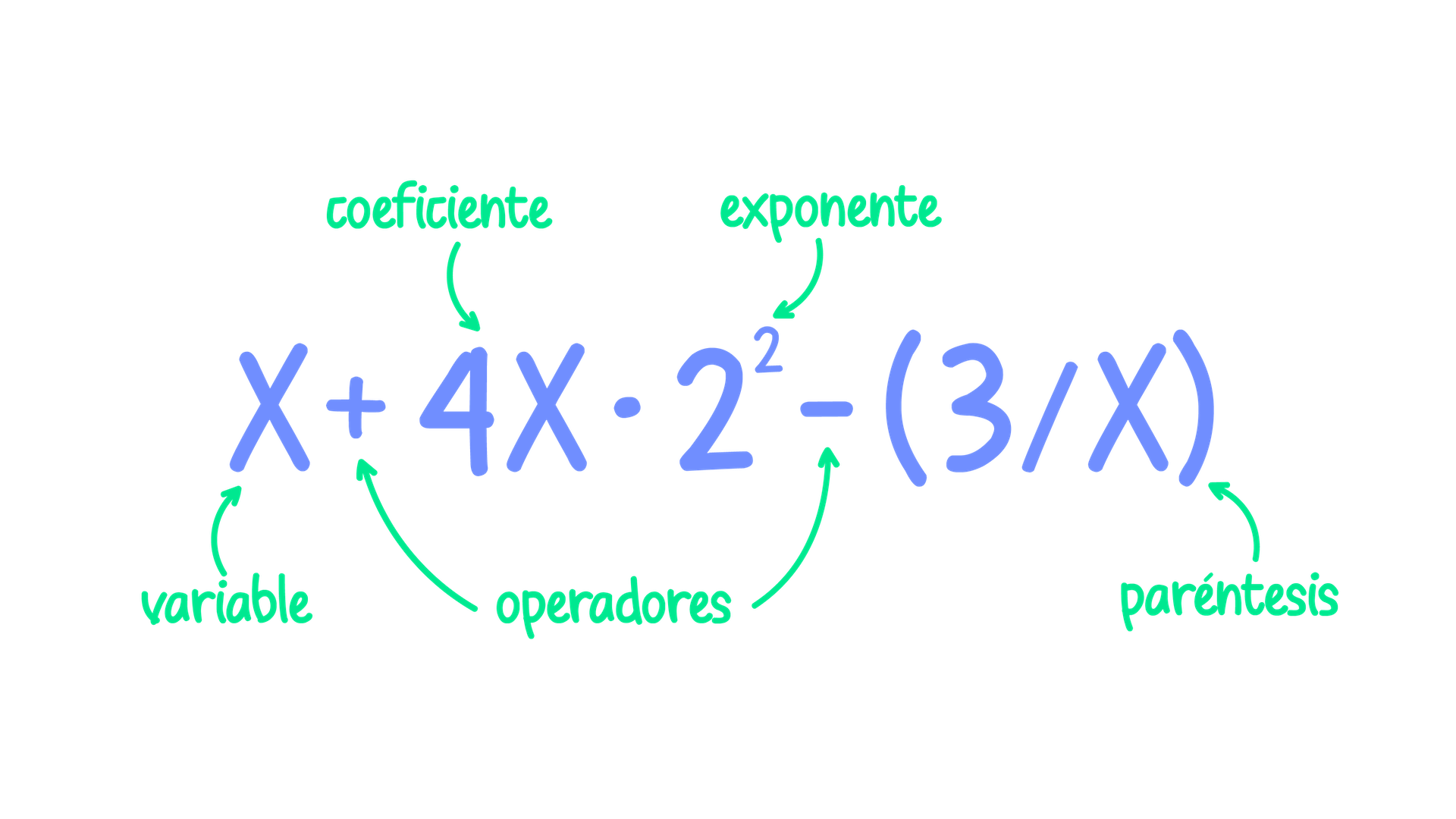
Cuando se trabaja en algebra se esta hablando de manejar relaciones numericas en la que una o mas cantidades son desconocidas. Las cuales son llamadas incognitas, variables o indeterminadas, que suelen representar con letras de la A-Z aunque la mas comun casi siempre es X.
Valor numerico.
El valor numérico de una expresión algebraica es el número que resulta de sustituir las variables de la de dicha expresión por valores concretos y completar las operaciones. Una misma expresión algebraica puede tener muchos valores numéricos diferentes, en función del número que se asigne a cada una de las variables de la misma
La única precaución necesaria es respetar el orden y las propiedades de las operaciones. Por ejemplo, no tiene sentido calcular el valor numérico de 1/x para , porque no se puede dividir entre cero.
En el siguiente ejemplo puedes ver cómo se haría la sustitución para calcular el valor numérico de para x=2 y= -1 z=4
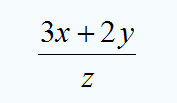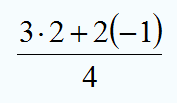
Faltaría completar las operaciones (el resultado final es ), pero lo más importante es que te fijes en los elementos que se añaden al hacer la sustitución: Se sustitulle en el punto de la x el valor de 2 en la y el valor de -1 y en la z el valor de 4 como indica el ejercicio.
SUMA Y RESTA
Suma:
Para sumar expresiones algebraicas, hay que tener en cuenta dos cosas, la suma de dos términos semejantes se pueden reducir a un solo termino, si tales términos son diferentes ante una suma, simplemente el resultado se deja expresada tal cual es sin cambiar los signos de los términos.
Para la suma de una expresion algebraica tenemos que entender que el coheficiente es totalmente modificable dependiendo la cantidad que nos de la suma, mas la variable se mantiene siempre en cuanto sea la misma de la que se esta sumando.
Ejemplo 1
Ejemplo 2
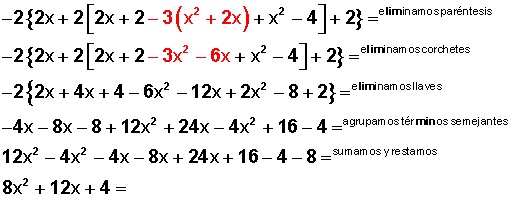
Resta:
En general, la resta o sustracción consiste en, dada cierta cantidad, eliminar una parte de ella, y el resultado se conoce como diferencia o resto. Es la operación inversa a la suma.
Para la resta de una expresion algebraica tenemos que entender que el coheficiente es totalmente modificable dependiendo la cantidad que nos de la resta, mas la variable se mantiene siempre en cuanto sea la misma de la que se esta restando.
Ejemplo 1
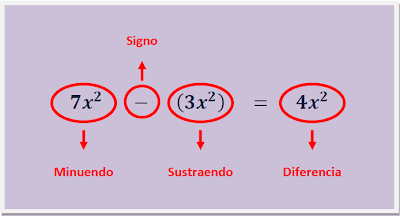
Ejemplo 2:
El blog de Matemáticas 