Suma y resta de fracciones algebraicas.
El procedimiento es el mismo que para sumar o restar fracciones numéricas, es decir, necesitamos tener el mismo denominador para sumar y restar fracciones y cuando no lo tenemos, tenemos que reducir las fracciones a denominador común, con la diferencia de que con las fracciones algebraicas, en vez de números, trabajamos con polinomios.
Vamos a verlo paso a paso.
suma y resta de fracciones algebraicas de igual denominador
Empezamos con la suma y resta de fracciones algebraicas que tienen el mismo denominador, como por ejemplo ésta:

En este caso, se mantiene el denominador y se opera con los numeradores. Podemos dejar una sola fracción con el denominador común y con los términos de ambos numeradores:

Y después agrupar términos semejantes en el numerador:

Sumar y restar fracciones algebraicas que tienen el mismo denominador es así de sencillo. Sin embargo, hay que tener mucho cuidado en la resta de fracciones algebraicas, ya que el signo menos, afecta a todos los términos del numerador de la fracción que tenga detrás.
Vamos a ver un ejemplo con resta de fracciones algebraicas para que lo entiendas mejor:
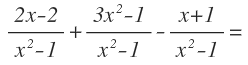
Tenemos el mismo denominador y por tanto, podemos unir todos los numeradores en uno sólo. Pero ahora, delante de la última fracción tenemos un signo menos y como te comentaba antes, afecta a los dos términos del numerador de la fracción que tiene detrás. Por tanto, para que siga siendo así, los términos afectados por el signo menos deben ir encerrados entre paréntesis:

En el siguiente paso, eliminamos el paréntesis, cambiando de signo a los términos que tiene dentro:

Y por último, agrupamos términos semejantes en el numerador:
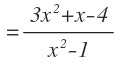
Un error muy común es no encerrar entre paréntesis los términos del numerador de la fracción que está precedida por un signo menos. En caso de no hacerlo, solamente le cambiamos el signo al primer término, lo cual es un error:

les dejo este video de apoyo:
Suma y resta de fracciones algebraicas con distinto denominador
Ten en cuenta que sólo se pueden sumar o restar fracciones algebraicas que tengan el mismo denominador, por lo que si tienen distinto denominador, antes hay que reducirlas a común denominador, para sumar o restar fracciones numéricas con distinto denominador.
Obtenemos el denominador común calculando el mínimo común múltiplo de los denominadores.
Por ejemplo, tenemos sumas y restas de fracciones algebraicas, cuyos denominadores no son iguales:

El primer paso será reducirlas a denominador común calculando el mínimo común múltiplo de los denominadores:

Para ello, previamente, hay que descomponer los polinomios. Los polinomios de la segunda y la tercera fracción algebraica no se pueden descomponer por ser de grado 1. Descomponemos el denominador de la primera fracción y nos queda:

Por tanto, tenemos los factores (x+1) y (x-1), sin ningún exponente (o elevados a 1), por lo que el mínimo común múltiplo será la multiplicación de ambos:
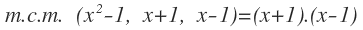
Vamos a transformar cada fracción algebraica que ya teníamos en una fracción algebraica equivalente con el denominador común que acabamos de calcular.
Colocamos nuestro nuevo denominador en cada una de las fracciones, listo para empezar a calcular el nuevo numerador de cada fracción:
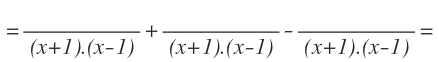
Para transformar una fracción algebraica en otra que sea equivalente, tenemos que multiplicar el numerador y el denominador por el mismo polinomio.
Al colocar el denominador común directamente, ya hemos multiplicando el denominador original por un polinomio, por lo que falta multiplicar el numerador por el mismo polinomio para que la fracción algebraica sea equivalente.
¿Cómo obtenemos ese polinomio por el que hay que multiplicar cada numerador?
Se obtiene dividiendo el denominador común entre el denominador original de cada fracción algebraica:
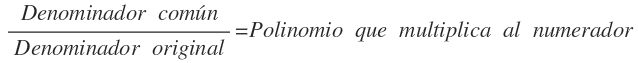
Vamos a verlo con la primera fracción algebraica de la operación del ejemplo:
Inicialmente teníamos en el denominador el polinomio (x²-1) y en la nueva fracción equivalente tenemos como denominador (x+1).(x-1):

Vamos a verlo con la primera fracción algebraica de la operación del ejemplo:
Inicialmente teníamos en el denominador el polinomio (x²-1) y en la nueva fracción equivalente tenemos como denominador (x+1).(x-1):

Si calculamos el polinomio por el que multiplicar el numerador mediante la fórmula anterior, obtenemos ese 1:

Vamos a ver cuál es el polinomio por el que tenemos que multiplicar la segunda fracción:

Teníamos como denominador original (x+1) y ahora tenemos (x+1).(x-1) que es el denominador común. Al dividir el denominador común entre el denominador original nos queda (x-1):

Que es el polinomio por le que tenemos que multiplicar el numerador para que la fracción algebraica sea equivalente a la original:

Y por último, hacemos lo mismo con la tercera fracción algebraica:

Dividimos el denominador común entre el denominador original:
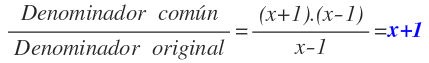
De esta forma hemos obtenido las tres fracciones algebraicas equivalentes con el denominador común:
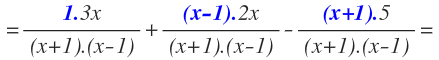
Ya tienen el mismo denominador y por tanto, ya se pueden sumar y restar, pero antes, multiplicamos en los numeradores:

Ahora ya podemos unir todos los numeradores en una sola fracción con el denominador común. Ten en cuenta, como siempre, que el signo menor afecta a todos los términos del numerador que tiene detrás y por eso, debemos encerrar esos términos entre paréntesis (no me cansaré de repetirlo):

Eliminamos el paréntesis del numerador:

Agrupamos términos en el numerador y en el último paso, multiplicamos en el denominador para obtener el resultado final:

Para una mejor comprensión les coloco este video
Multiplicación y división de fracciones algebraicas.
A continuación te voy a enseñar con todo detalle cómo multiplicar y dividir fracciones algebraicas, con ejercicios resueltos paso por paso.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
para empezar sería bueno ver este video que nos ayudará mucho con este tema.
Multiplicación de fracciones algebraicas.
Las fracciones algebraicas se multiplican igual que las fracciones numéricas, es decir se multiplican en linea; numerador por numerador y denominador por denominador, solo que en este caso, en vez de números tenemos polinomios:
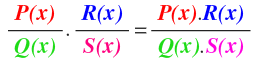
Hay que tener en cuenta también otra pequeña diferencia (aunque es sólo una recomendación) que te paso a explicar:
En la multiplicación de fracciones numéricas, se multiplican los números en línea y al final se simplifica la fracción. Con fracciones algebraicas, podemos hacerlo igual, pero las operaciones se complicarían demasiado.
Así que, lo que yo recomiendo es que antes de multiplicar,descompongamos los polinomios y eliminemos los factores que se repitan en el numerador y el denominador, es decir, que simplifiquemos antes de multiplicar.
Una vez hemos eliminado todos los factores repetidos, ya podemos multiplicar tanto en el numerador como en el denominador, para mostrarlo en el resultado. Es decir, multiplicamos al final.
Vamos a resolver un ejemplo paso a paso, para que te quede más claro lo que te acabo de decir.
Tenemos la siguiente multiplicación de fracciones algebraicas:
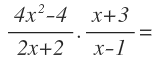
Al ser una multiplicación de fracciones, multiplicamos en línea, es decir, numerador por numerador y denominador por denominador, pero al ser polinomios, solamente lo dejamos indicado, no los multiplicamos:
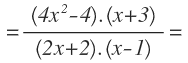
Antes de multiplicar, vamos a descomponer los polinomios que se puedan descomponer. Empezamos por el polinomio correspondiente al numerador de la primera fracción:

Descomponemos también el polinomio del denominador de la primer fracción:
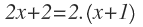
Los otros dos polinomios no se pueden descomponer, al ser ya de grado 1.
Sustituimos los polinomios por sus correspondientes descomposiciones:

Ahora simplificamos la fracción algebraica, eliminando los factores que se repiten en el numerador y en el denominador:
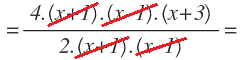
Y nos queda:
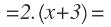
Que multiplicamos para obtener el resultado final:

Si hubiésemos multiplicado al principio, al final nos hubieran quedado dos polinomios de mayor grado, los cuales hubiera sido mucho más difícil de factorizar.
Siguiendo este procedimiento, llegamos al resultado mucho más directamente.
de nuevo tenemos este video de refuerzo.
Vamos a ver ahora la división de fracciones algebraicas.
División de fracciones algebraicas
La división de fracciones algebraicas también se realiza igual que una división de fracciones numéricas, es decir, hay 3 formas de hacerlo: multiplicación en forma de cruz, multiplicando en forma de oreja y la ultima es invirtiendo el divisor. En esta ocasión utilizaremos la segunda forma.
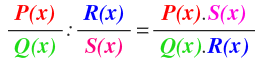
Como en el caso de la multiplicación, también conviene dejar la multiplicación indicada y factorizar los polinomios antes de realizar la multiplicación, para llegar al resultado simplificado de una manera más directa.
Vamos a verlo con otro ejemplo:

Al ser una división de fracciones algebraicas, multiplicamos los polinomios en cruz y lo dejamos indicado (sin llegar a realizar la multiplicación de polinomios):

Ahora descomponemos los polinomios
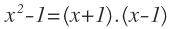


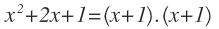
Uno de los polinomios del numerador no se puede descomponer aunque es de grado 2, ya que su función no tiene soluciones raíces.
Sustituimos cada polinomio por su descomposición:

Eliminamos los factores que se repiten en el numerador y en el denominador:

Y nos queda:
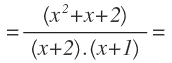
Por último, multiplicamos los factores que tenemos en el denominador para obtener el resultado final:
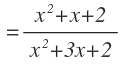
En el caso de la división, al descomponer los polinomios antes de multiplicar en cruz, también obtenemos un resultado simplificado directamente.
Ejercicios propuestos

por último espero sea de mucha ayuda.